Implementing OrderedMap in Go 2.0 by Using Generics with Delete Operation in O(1) Time Complexity

Probably the most sought after feature of Go programming language, Generics, is on its way and is expected to land with v2. You can check out the proposal here, and have a play with it in Go playground for v2. I stumbled upon rocketlaunchr.cloud's great post on using generics in Go 2, and the post shows how you can implement ordered maps. The post is very informative, and shows you how powerful Generics will be for Go.

However, I noticed a performance issues with the implementation of Delete operation on the OrderedMap struct, and in this post, I want to show a much better implementation in terms of time complexity with a Doubly Linked List data structure, and show the impact of the change.

The Problem

To summarize the current approach in rocketlaunchr.cloud's post, it essentially exposes the below signature:

type OrderedMap[type K comparable, V any] struct {
	store map[K]V
	keys  []K
}

func (o *OrderedMap[K, V]) Get(key K) (V, bool) {
    // ...
}

func (o *OrderedMap[K, V]) Set(key K, val V) {
    // ...
}

func (o *OrderedMap[K, V]) Delete(key K) {
    // ...
}

func (o *OrderedMap[K, V]) Iterator() func() (*int, *K, V) {
    // ...
}

The implementation also gives the FIFO guarantee through the iterator and maintaining the order of the list even after the delete operation (e.g. if the map has 1,2,3,4, and 3 is then deleted, the iterator will output the data with the following order 1,2,4.).

The performance problem with the implementation is with the Delete method, which has the below implementation:

func (o *OrderedMap[K, V]) Delete(key K) {
	delete(o.store, key)

	// Find key in slice
	var idx *int

	for i, val := range o.keys {
		if val == key {
			idx = &[]int{i}[0]
			break
		}
	}
	if idx != nil {
		o.keys = append(o.keys[:*idx], o.keys[*idx+1:]...)
	}
}

The implementation here is iterating over the entire keys slice to perform the delete operation, which has O(N) time complexity and this can be a significant performance hit where there is a need to store large collections while making use of the Delete operation frequently. We can also observe that we are performing a shift in the keys slice as well, with the below operation

if idx != nil {
    o.keys = append(o.keys[:*idx], o.keys[*idx+1:]...)
}

o.keys[:*idx], o.keys[*idx+1:] and append all here have its own time complexity, and depending on how much the backing array needs to grow, the complexity of this operation can grow. That said, I have to admit that the language features here make it hard to reason about the exact time complexity of each operation here.

In the post, I realized that rocketlaunchr.cloud actually calls for an action for readers to address this known issue with the below quote for this :)

Currently, when you delete a key-value pair, you need to iterate over the keys slice to find the index of the key you want to delete. You can use another map that associates the key to the index in the keys slice. I’ll leave it to the reader to implement.

Thinking about this now and it won't actually be enough for us to store the index as it will require us to perform either shift the slice where the keys are stored, or keep the storage for deleted keys and skip them during iteration. Both has its own disadvantages where the first option will have time complexity hit per each delete operation, whereas the second one will both increase the time complexity of iterator as well as increasing the space complexity.

Doubly Linked List Data Structure to Rescue

It's actually possible to reduce the time complexity of the Delete operation to O(1) by changing the way how we store the data within the implementation of OrderedMap struct, without increasing the time complexity of other operations, and needing to change any of its public signature. We can do this by storing the ordered data in a Doubly Linked List data structure, and storing each node in the map as the value, instead of the raw value.

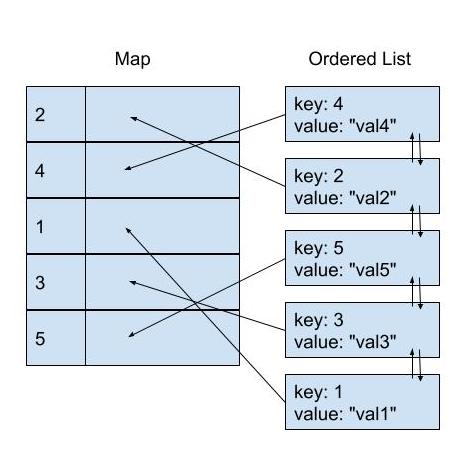
Implementation of a Doubly Linked List data structure should be fairly straight forward to implement. However, Go already has one under container/list package. The only caveat for us with this one is that there is no generic version of this in Go 2 at the moment, as far as I am aware. That said, we actually don't need a generic version of this since we will use this internally within the scope of OrderedMap, and we can store the value as interface{} instead.

Implementation

Let's look at the implementation, going through it step by step. Below we can see how we are changing the internal state storage constructs of the OrderedMap struct as well as its construction:

type OrderedMap[type K comparable, V any] struct {
	store map[K]*list.Element
	keys  *list.List
}

func NewOrderedMap[type K comparable, V any]() *OrderedMap[K, V] {
	return &OrderedMap[K, V]{
		store: map[K]*list.Element{},
		keys:  list.New(),
	}
}

The biggest changes to notice here are:

• keys type has changed from []K to *list.List
• map type has changed from map[K]V to map[K]*list.Element, where we are now storing the doubly linked list node, instead of the raw value

These changes to the internal storage will impact the implementation of all methods, but without increasing the time complexity, and needing to change the public signature of each method. Below, for example, is how the Set and Get method implementations have changed:

type keyValueHolder[type K comparable, V any] struct {
	key K
	value V
}

func (o *OrderedMap[K, V]) Set(key K, val V) {
	var e *list.Element
	if _, exists := o.store[key]; !exists {
		e = o.keys.PushBack(keyValueHolder[K, V]{
			key: key,
			value: val,
		})
	} else {
		e = o.store[key]
		e.Value = keyValueHolder[K, V]{
			key: key,
			value: val,
		}
	}
	o.store[key] = e
}

func (o *OrderedMap[K, V]) Get(key K) (V, bool) {
	val, exists := o.store[key]
	if !exists {
		return *new(V), false
	}
	return val.Value.(keyValueHolder[K, V]).value, true
}

func (o *OrderedMap[K, V]) Iterator() func() (*int, *K, V) {
	e := o.keys.Front()
	j := 0
	return func() (_ *int, _ *K, _ V) {
		if e == nil {
			return
		}

		keyVal := e.Value.(keyValueHolder[K, V])
		j++
		e = e.Next()

		return func() *int { v := j-1; return &v }(), &keyVal.key, keyVal.value
	}
}

In a nutshell, the difference here is that we are storing the doubly linked list node as the value in the map, and we store both the key and value as the value of the doubly linked list node through keyValueHolder struct. This obviously impacts how we set and get the data, but the time complexity of both the methods stay as O(1). We will actually observe the biggest change with the Delete method here:

func (o *OrderedMap[K, V]) Delete(key K) {
	e, exists := o.store[key]
	if !exists {
		return
	}

	o.keys.Remove(e)

	delete(o.store, key)
}

If we were to break this down, here is what we are doing here:

• Accessing the doubly linked list node from the map first, based on the given key. This is O(1) in terms of time complexity.
• Calling Remove on the doubly linked list by passing the found element. This is O(1) in terms of time complexity.
• Deleting node from the map, based on the given key. This is also O(1) in terms of time complexity.

One more thing to unwrap here is how come calling Remove on the doubly linked list is O(1) in terms of time complexity, and showing its implementation might shed some light on the rationale:

// Remove removes e from l if e is an element of list l.
// It returns the element value e.Value.
// The element must not be nil.
func (l *List) Remove(e *Element) interface{} {
	if e.list == l {
		// if e.list == l, l must have been initialized when e was inserted
		// in l or l == nil (e is a zero Element) and l.remove will crash
		l.remove(e)
	}
	return e.Value
}

// remove removes e from its list, decrements l.len, and returns e.
func (l *List) remove(e *Element) *Element {
	e.prev.next = e.next
	e.next.prev = e.prev
	e.next = nil // avoid memory leaks
	e.prev = nil // avoid memory leaks
	e.list = nil
	l.len--
	return e
}

All that this implementation does is to appropriately remove the links from the node that we want to remove, and wiring up its next node with its previous node (if they exist). You can also see this implementation here in Go source code.

You can also see the whole implementation working here in Go 2 Playground:

0 1 string1 is a string
1 2 string2 is a string
2 4 string4 is a string

Program exited.

Benchmarking to Show the Impact

To be able to understand the improvement we have made here, we can run a benchmark between the two Delete implementations with Go's built-in benchmark tooling. For this, we will go with the below benchmark setup:

• Sequential input of an array with 1M items
• Seeding the OrderedMap with these 1M items
• Deleting a random key for 100K times

One caveat with the benchmark here is that we will run it with non-generic implementations since I wasn't unable to find a way to install Go 2 on my machine to be able to run a benchmark, and I don't believe it's possible to run one with Go playground. That said, this shouldn't change anything for us to be able to understand the difference between two Delete implementations as the logic will stay the same. The only change will be that the usage of the type will not be obvious due to lack of strongly typed signature. I have put the OrderedMap with original Delete implementation here, and with the improved one here.

The code for the benchmark itself is as below (which you can also find here):

package main

import (
	"fmt"
	"math/rand"
	"testing"
)

func BenchmarkOrderedMapLinkedListBasedDelete(b *testing.B) {
	for n := 0; n < b.N; n++ {
		seedCount := 1000000
		m := NewLinkedListBasedOrderedMap()
		for i := 1; i <= seedCount; i++ {
			m.Set(i, fmt.Sprintf("string%d", i))
		}
		for i := 0; i < 100000; i++ {
			m.Delete(rand.Intn(seedCount-1) + 1)
		}
	}
}

func BenchmarkOrderedMapSliceBasedDelete(b *testing.B) {
	for n := 0; n < b.N; n++ {
		seedCount := 1000000
		m := NewOrderedMap()
		for i := 1; i <= seedCount; i++ {
			m.Set(i, fmt.Sprintf("string%d", i))
		}
		for i := 0; i < 100000; i++ {
			m.Delete(rand.Intn(seedCount-1) + 1)
		}
	}
}

We can run this benchmark with go test command. However, note that the exact time that takes to run each function is not significant here, since it will depend on the machine spec, etc. Also, in the test, we are seeding the map implementations for each run, which means extra time we are adding to the exact time to run the function. That said, what's important to observe here is the difference in time between two functions:

➜  ordered-map-generics git:(master) ✗ go test -bench=BenchmarkOrderedMap -benchtime=30s
goos: darwin
goarch: amd64
pkg: github.com/tugberkugurlu/algos-go/ordered-map-generics
BenchmarkOrderedMapLinkedListBasedDelete-4   	      42	 724271767 ns/op
BenchmarkOrderedMapSliceBasedDelete-4        	       1	54509739278 ns/op
PASS
ok  	github.com/tugberkugurlu/algos-go/ordered-map-generics	86.361s

Wow, we can see the orders of magnitude improvement here, and it's very rewarding to see the impact.

Conclusion

The biggest take away from this post I believe is how Generics will change the way we can implement more complex and powerful data structures, and allow them to be reused more effectively by truly taking advantage of strongly-typed nature of Go, as well as how important it's to use the correct data structures for the expected usage of own types. As a side note, I thoroughly enjoyed writing this post, as I was able to feel the power of having Generics available to use in Go!